|
Wave Reflection at an Impedance
Discontinuity(阻抗不连续性处的反射)
The impedance for mechanical waves is defined as the ratio
between the force wave and velocity wave and in general takes
the for
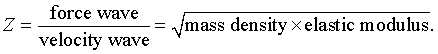
For transverse waves in a string with linear mass density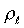
(kg/m) and tension T (N), the impedance is
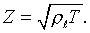
If two strings with different
mass densities are connected with a common tension, the
impedance discontinuity at the joint causes wave reflection. For
an incident displacement wave of unit amplitude in string 1, the
reflected wave is
and transmitted wave is
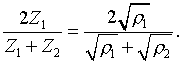
The first animation shows
reflection and transmission of incident pulse wave of unit
amplitude when the mass density ratio is 4, Z1/Z2 = 1/2. The
reflected wave is negative and its peak is -1/3. The transmitted
wave, which propagates slower, has an amplitude of 1 - 1/3 =
+2/3, as expected from the formulae.
The second animation shows the case Z1/Z2 = 2, i.e., the
incident wave is in a heavier string. There is no sign reversal
in the reflected wave in this case. The transmitted wave has an
amplitude larger than the incident wave. This does not mean
amplification in wave energy. (Why not?)
The third animation shows reflection at a fixed end (Z2 =
infinity) and fourth animation shows reflection at a free end
(Z2 = 0).
Reflection of pulse wave at an impedenace discontinuity when
Z_1/Z_2 = 0.5.
> with(plots):
animate((exp(-(x-t)^2)-1/3*exp(-(x+t)^2))*Heaviside(-x)+2/3*exp(-4*(x-.5*t)^2)*Heaviside(x),x=-10..10,t=-10..10,frames=50,color=red,numpoints=200);
When Z_1/Z_2 = 2.0.
> with(plots):
animate((exp(-(x-t)^2)+1/3*exp(-(x+t)^2))*Heaviside(-x)+4/3*exp(-.25*(x-2*t)^2)*Heaviside(x),x=-10..20,t=-10..10,frames=50,color=red,numpoints=200);
When Z_2 = infinity. (Fixed end)
> with(plots):
animate((exp(-(x-t)^2)-exp(-(x+t)^2)),x=-10..0,t=-10..10,frames=50,color=red,numpoints=200);
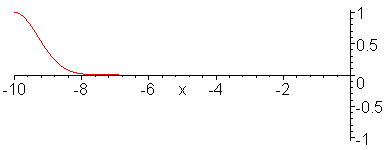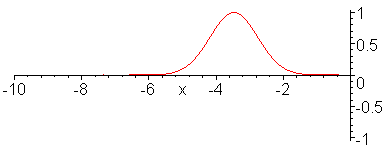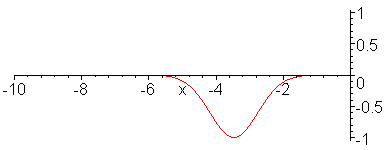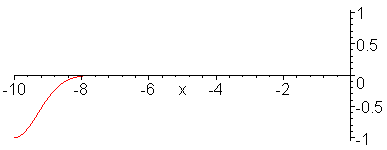
When Z_2 = 0. (Free end)
>
animate((exp(-(x-t)^2)+exp(-(x+t)^2)),x=-10..0,t=-10..10,frames=50,color=red,numpoints=200);
 |
